Вычислить координаты середины отрезка AB если A(1, 3, 4), B(5, 6, 1).

xc=1+52=62=3\displaystyle{ x_c = \frac{1+5}{2} = \frac{6}{2}=3}
yc=3+62=92=4.5\displaystyle{ y_c = \frac{3+6}{2} = \frac{9}{2}=4.5}
zc=4+12=52=2.5\displaystyle{ z_c = \frac{4+1}{2} = \frac{5}{2}=2.5}
Ответ: координаты середины отрезка AB точка C(3, 4.5, 2.5).
Введите координаты точки A
Введите координаты точки B
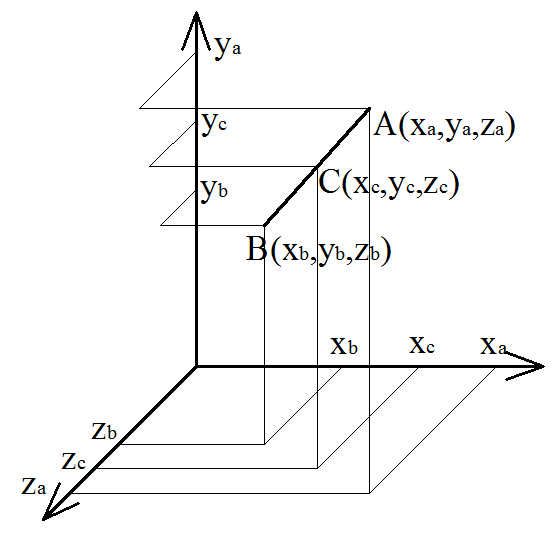
Координаты середины отрезка в пространстве

Формула расчёта координаты середины отрезка в пространстве

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

xc=xa+xb2\displaystyle {x_c = \frac{x_a + x_b}{2}}
yc=ya+yb2\displaystyle {y_c = \frac{y_a + y_b}{2}}
zc=za+zb2\displaystyle {z_c = \frac{z_a + z_b}{2}}
A(xa,ya,za)A(x_a, y_a, z_a), B(xb,yb,zb)B(x_b, y_b, z_b) - координаты концов отрезка
C(xc,yc,zc)C(x_c, y_c, z_c) - координаты середины отрезка
Найти координаты середины отрезка AB если A(0, 2, 3), B(6, 5, 0).
Найти координаты середины отрезка AB если A(3, 6, 4), B(1, 2, 2).
Найти координаты середины отрезка AB если A(6, 1, 5), B(0, 4, 3).
Найти координаты середины отрезка AB если A(3, 1, 4), B(6, 5, 2).
Похожие калькуляторы
Координаты середины отрезка на плоскости