Уравнение прямой проходящей через две точки на плоскости
Онлайн калькулятор составляет уравнение прямой проходящей через 2 точки на плоскости. Подробное решение с пояснением.
Вывод формулы уравнения прямой по двум точкам
Общее уравнение прямой на плоскости
Уравнение вида Ax+By+C=0 где A и B одновременно не равны 0 определяет прямую.
Частные случаи общего уравнения прямой
| Значения коэффициентов | Уравнение прямой | Положение прямой | |
| 1 | A≠0, B≠0, C=0 | Ax+By=0 | Прямая проходит через начало координат |
| 2 | A=0, B≠0, C≠0 | By+C=0 ⇒ y=-C/B | Прямая будет параллельна оси x |
| 3 | A≠0, B=0, C≠0 | Ax+C=0 ⇒ x=-C/A | Прямая будет параллельна оси y |
| 4 | A=0, B≠0, C=0 | By=0 ⇒ y=0 | Прямая будет совпадать с осью x |
| 5 | A≠0, B=0, C=0 | Ax=0 ⇒ x=0 | Прямая будет совпадать с осью y |
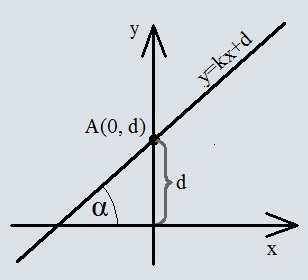
Уравнение прямой с угловым коэффициентом
Уравнение вида y=kx+d, где k является угловым коэффициентом а d некоторым числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой непараллельной оси y.
k - угловой коэффициент равный k=tg(α)
Подставим координаты точки A(0, d) в уравнение y=kx+d. Получится d=k×0+d, отсюда мы можем сделать вывод что прямая вида y=kx+d проходит через точку A(0, d).
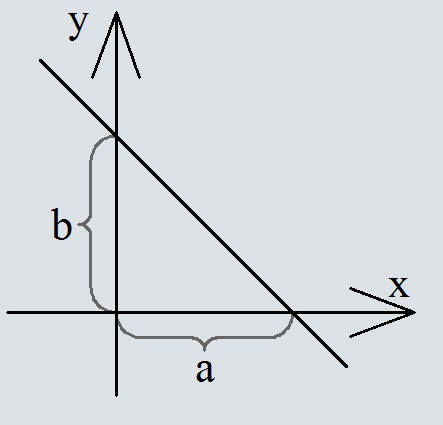
Уравнение прямой в отрезках
Уравнение вида x/a+y/b=1, где a и b некоторые числа отличные от нуля, называют уравнением прямой в отрезках. Величины чисел a и b являются длинами отрезков отсекаемых этой прямой от осей ox и oy. Длины отрезков считаются от начала координат.
Знак − означает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.