Расчёт периметра квадрата по радиусу описанной окружности
Диаметр описанной квадрат окружности равен диагонали квадрата.
Периметр квадрата равен сумме длин четырёх его сторон.
Квадрат это прямоугольник у которого все стороны и углы равны.
Калькулятор рассчитывает периметр квадрата по радиусу описанной окружности.
Периметр квадрата равен сумме длин четырёх его сторон.
Квадрат это прямоугольник у которого все стороны и углы равны.
Калькулятор рассчитывает периметр квадрата по радиусу описанной окружности.
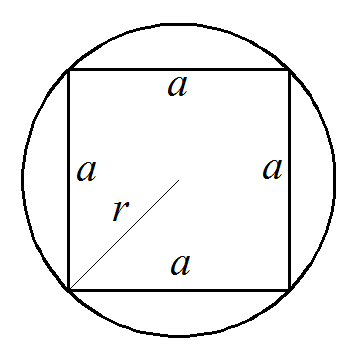
Так как диаметр описанной квадрат окружности равен диагонали квадрата. Найдём сторону квадрата по теореме пифагора.
\color{#0000FF}{{(2 \times r)}^2 = a^2 + a^2}
\color{#0000FF}{{(2 \times r)}^2 = 2 \times a^2}
\color{#0000FF}{a = \sqrt{\frac{ {(2 \times r)}^2 }{ 2 }}}
Cоответственно периметр будет
\color{#0000FF}{P = \sqrt{\frac{ {(2 \times r)}^2 }{ 2 }} \times 4}
Значащих цифр:
Введите радиус
Периметр квадрата с радусом 81 описанной окружности
Периметр квадрата с радусом 82 описанной окружности
Периметр квадрата с радусом 44 описанной окружности
Периметр квадрата с радусом 5 описанной окружности
Периметр квадрата с радусом 16 описанной окружности
Периметр квадрата с радусом 45 описанной окружности
Периметр квадрата с радусом 82 описанной окружности
Периметр квадрата с радусом 44 описанной окружности
Периметр квадрата с радусом 5 описанной окружности
Периметр квадрата с радусом 16 описанной окружности
Периметр квадрата с радусом 45 описанной окружности
Похожие калькуляторы