Рассчитать онлайн периметр прямоугольника с диагоналями 7 и углом между ними 162 градуса

Формула периметра прямоугольника

\color{#0000FF}{P = 2a+2b}

\color{#0000FF}{P = 2(a+b)}

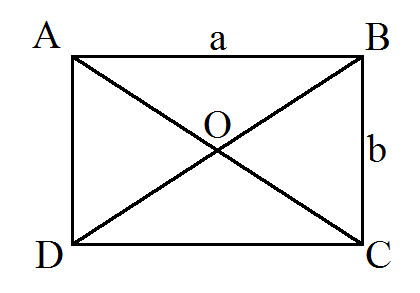
По теореме косинусов найдём стороны прямоугольника

\color{#0000FF}{{b}^2 = {BO}^2+{CO}^2-2*BO*CO*cos(BOC)}

Так как AO = BO = CO = DO упростим формулу выше

\color{#0000FF}{{b}^2 = 2*{AO}^2-2*{AO}^2*cos(BOC)}

\color{#0000FF}{{b}^2 = 2*{AO}^2*(1-cos(BOC))}

\color{#0000FF}{b = \sqrt{2*{AO}^2*(1-cos(BOC))}}

Так как углы AOB и BOC смежные AOB = 180 - BOC

\color{#0000FF}{a = \sqrt{2*{AO}^2*(1-cos(180-BOC))}}

Решение

\color{#0000FF}{a = \sqrt{2*{(\frac{7}{2})}^2*(1-cos(180-162))} = 1.09504126}

\color{#0000FF}{b = \sqrt{2*{(\frac{7}{2})}^2*(1-cos(162))} = 6.91381838}

\color{#0000FF}{P = 2(1.09504126+6.91381838) = 16.0177193}

Периметр прямоугольника с диагоналями 7 и углом между ними 162 равен 16.0177193

Ссылка на результат

https://calc-best.ru/matematicheskie/perimetry-figur/perimetr-pryamougolnika/po-diagonalyam-i-uglu-mezhdu-nimi?n1=7&n2=162

Значащих цифр:

Введите длину диагонали

Введите угол