Найти площадь прямоугольного треугольника с гепотенузой 17 и углом 18
Дано:
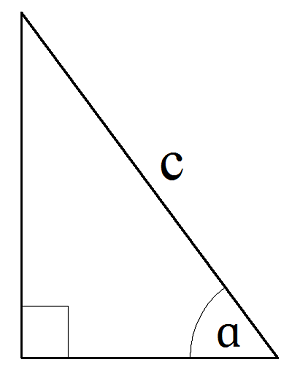
Прямоугольный треугольник
Гипотенуза c = 17
Острый угол α = 18
Решение:
Площадь прямоугольного треугольника с гипотенузой 17 и острым углом 18 равна 42.4674844781
Введите гипотенузу
Введите угол
Ссылка на результат
?n1=17&n2=18
Вычислить площадь прямоугольного треугольника с гипотенузой 18 и углом 3 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 1 и углом 7 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 10 и углом 74 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 7 и углом 18 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 3 и углом 82 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 1 и углом 28 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 15 и углом 3 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 1 и углом 7 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 10 и углом 74 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 7 и углом 18 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 3 и углом 82 градуса
Вычислить площадь прямоугольного треугольника с гипотенузой 1 и углом 28 градусов
Вычислить площадь прямоугольного треугольника с гипотенузой 15 и углом 3 градуса