Рассчитать высоту треугольника со сторонами 143, 116 и 80

Значащих цифр:

Введите длину стороны a

Введите длину стороны b

Введите длину стороны c

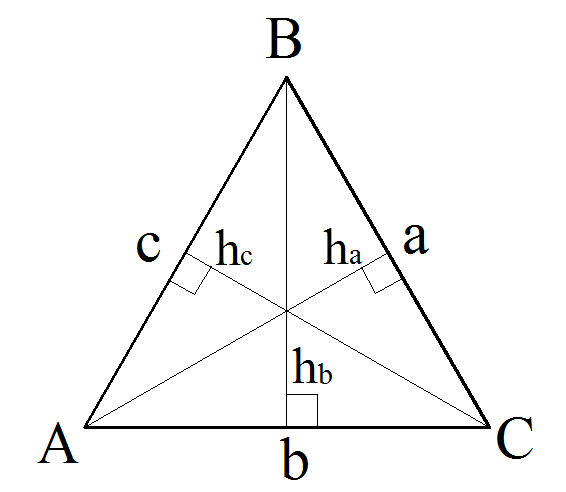
Формулу высоты треугольника выведем из формулы Герона

\color{#0000FF}{p = \Large{\frac{a + b + c}{2}}}

\color{#0000FF}{S = \sqrt{p(p-a)(p-b)(p-c)}}

Где a, b, c - длины сторон треугольника, p - полупериметр

и формулы площади треугольника

\color{#0000FF}{S = \Large\frac{1}{2}\normalsize*b*h_b}

Выведем высоту треугольника

\color{#0000FF}{\Large\frac{1}{2}\normalsize*b*h_b = \sqrt{p(p-a)(p-b)(p-c)}}

Формулы высот треугольника

\color{#0000FF}{h_b = \Large\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{b}}

\color{#0000FF}{h_a = \Large\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}}

\color{#0000FF}{h_c = \Large\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}}

Решение

\color{#0000FF}{p = \Large{\frac{143 + 116 + 80}{2}} \normalsize = 169.5}

\color{#0000FF}{h_b = \Large\frac{2\sqrt{169.5(169.5-143)(169.5-116)(169.5-80)}}{116}\normalsize = 79.9591564}

\color{#0000FF}{h_a = \Large\frac{2\sqrt{169.5(169.5-143)(169.5-116)(169.5-80)}}{143}\normalsize = 64.861973}

\color{#0000FF}{h_c = \Large\frac{2\sqrt{169.5(169.5-143)(169.5-116)(169.5-80)}}{80}\normalsize = 115.940777}

Высота треугольника опущенная с вершины B на сторону AC со сторонами 143, 116 и 80 равна 79.9591564

Высота треугольника опущенная с вершины A на сторону BC со сторонами 143, 116 и 80 равна 64.861973

Высота треугольника опущенная с вершины C на сторону AB со сторонами 143, 116 и 80 равна 115.940777

Ссылка на результат

?n1=143&n2=116&n3=80