Рассчитать онлайн периметра квадрата по радиусу 30 описанной окружности

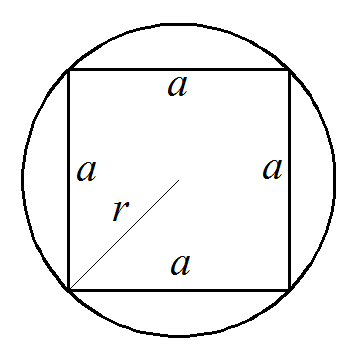
Периметр квадрата по радиусу 30 описанной окружности равен 169.705627.

Так как диаметр описанной квадрат окружности равен диагонали квадрата. Найдём сторону квадрата по теореме пифагора.

\color{#0000FF}{{(2 \times r)}^2 = a^2 + a^2}

\color{#0000FF}{{(2 \times r)}^2 = 2 \times a^2}

\color{#0000FF}{a = \sqrt{\frac{ {(2 \times r)}^2 }{ 2 }}}

Cоответственно периметр будет

\color{#0000FF}{P = \sqrt{\frac{ {(2 \times r)}^2 }{ 2 }} \times 4}

\color{#0000FF}{P = \sqrt{\frac{ {(2 \times 30)}^2 }{ 2 }} \times 4 = 169.705627}

Значащих цифр:

Введите радиус

Похожие калькуляторы