Найти периметр равнобедренного треугольника по основанию 40 и высоте 40

Дано:
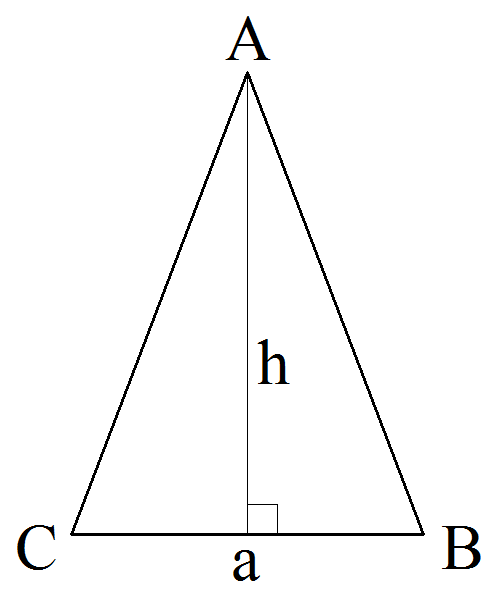
Равнобедренный треугольник
Основание a = 40
Высота h = 40
Решение:
По теореме Пифагора найдём длину боковой стороны
Вычислим периметр сложив все стороны
Периметр равнобедренного треугольника с основанием 40 и высотой 40 равен 129.4427
Введите основание
Введите высоту
Периметр равнобедренного треугольника по основанию и высоте
Вычислить периметр равнобедренного треугольника с основанием 33 и высотой 31
Вычислить периметр равнобедренного треугольника с основанием 44 и высотой 2
Вычислить периметр равнобедренного треугольника с основанием 14 и высотой 13
Вычислить периметр равнобедренного треугольника с основанием 24 и высотой 27
Вычислить периметр равнобедренного треугольника с основанием 12 и высотой 10
Вычислить периметр равнобедренного треугольника с основанием 20 и высотой 10
Вычислить периметр равнобедренного треугольника с основанием 16 и высотой 37
Похожие калькуляторы
Периметр прямоугольного треугольника по катету и противолежащему углу
Периметр прямоугольного треугольника по катету и прилежащему углу
Периметр прямоугольного треугольника по гипотенузе и углу
Периметр равностороннего треугольника по площади вписанной окружности
Периметр треугольника по двум сторонам и углу между ними
Периметр равностороннего треугольника по высоте
Периметр равнобедренного треугольника по боковой стороне и основанию
Периметр прямоугольного треугольника по катетам
Периметр прямоугольного треугольника по катету и гипотенузе
Периметр треугольника по средним линиям
Периметр треугольника по сторонам