Вычислить площадь прямоугольника по диагонали 54 и стороне 11

Дано
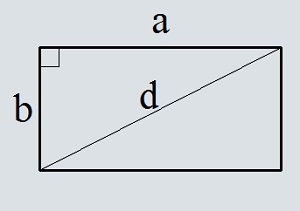
Прямоугольник с диагональю 54 и стороной 11
Задача
Вычислить площадь прямоугольника
Решение
Так как диагональ делит прямоугольник на 2 прямоугольных треугольника. В которых диагональ является гипотенузой а сторона катетом. Исходя из этого по теореме Пифагора вычислим сторону b.
d2=a2+b2\displaystyle {d^2=a^2+b^2}
b2=d2−a2\displaystyle {b^2=d^2-a^2}
b=d2−a2)\displaystyle {b=\sqrt{d^2-a^2)}}
Подставим полученную сторону в формулу площади прямоугольника
S=ab=ad2−a2)\displaystyle {S=ab=a\sqrt{d^2-a^2)}}
S=ad2−a2)\displaystyle {S=a\sqrt{d^2-a^2)}}
Подставим значения и вычислим
S=11×542−112)=581.545355067\displaystyle {S=11 \times \sqrt{54^2-11^2)}=581.545355067}
Площадь прямоугольника по диагонали 54 и стороне 11 равна 581.545355067
Площадь прямоугольника по диагонали и стороне
Введите диагональ d
Введите сторону a
Ссылка на результат
https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-pryamougolnika/po-diagonali-i-storone?n1=54&n2=11
Вычислить площадь прямоугольника по диагонали 76 и стороне 9
Вычислить площадь прямоугольника по диагонали 48 и стороне 41
Вычислить площадь прямоугольника по диагонали 75 и стороне 26
Похожие калькуляторы
Площадь прямоугольника по диагоналям и углу между ними
Площадь прямоугольника по сторонам