Вычислить площадь квадрата вписанного в окружность по известной площади этой окружности равной 22

Дано

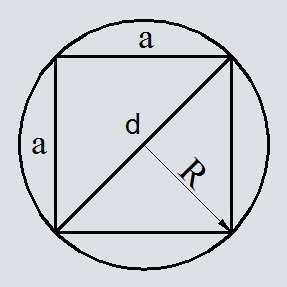
Окружность с вписанным квадратом

Площадь окружности S_окр = 22

Задача

Вычислить площадь квадрата

Решение

Из формулы площади окружности выведем радиус

\displaystyle {S_{okp}=\pi R^2}

\displaystyle {R=\sqrt{\frac{S_{okp}}{\pi}}}

С помощью теоремы Пифагора выведем сторону a

\displaystyle {a^2+a^2=d^2=(2R)^2=4R^2}

\displaystyle {a=\sqrt{2}R}

Подставим в формулу площади квадрата

\displaystyle {S=a^2=2R^2}

Подставим в формулу выведенный ранее радиус

\displaystyle {S=2R^2=\frac{2S_{okp}}{\pi}}

\displaystyle {S=\frac{2S_{okp}}{\pi}}

Подставим значение и вычислим

\displaystyle {S=\frac{2\times 22}{3.14}=14.0127388535}

Площадь квадрата вписанного в окружность, с площадью этой окружности 22 равна 14.0127388535

Площадь квадрата вписанного в окружность по известной площади этой окружности

Введите площадь окружности S_окр

Ссылка на результат

https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-kvadrata/vpisannogo-v-okruzhnost-po-izvestnoj-ploshchadi-okruzhnosti?n=22

Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 27
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 91
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 89
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 82
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 52
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 43
Вычислить площадь квадрата вписанного в окружность если площадь этой окружности равна 27

Похожие калькуляторы

Площадь квадрата через площадь окружности, вписанной в этот квадрат

Площадь квадрата через длину окружности, вписанной в этот квадрат

Площадь квадрата вписанного в окружность, по известной длине окружности

Площадь квадрата по радиусу вписанной окружности

Площадь квадрата по радиусу описанной окружности

Площадь квадрата по периметру

Площадь квадрата по стороне

Площадь квадрата по диагонали