Вычислить площадь ромба через радиус 15 вписанной окружности и угол 1 градус между сторонами

Дано
Ромб с углом между сторонами α=1
Вписанная окружность с радиусом R=15
Задача
Вычислить площадь ромба
Решение
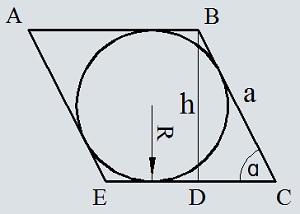
Из треугольника BCD выведем сторону a
sin(α)=ha\displaystyle {sin(\alpha)=\frac{h}{a}}
a=hsin(α)\displaystyle {a=\frac{h}{sin(\alpha)}}
Высота ромба равна диаметру вписанной окружности или двум радиусам
h=2R
a=hsin(α)=2Rsin(α)\displaystyle {a=\frac{h}{sin(\alpha)}=\frac{2R}{sin(\alpha)}}
Если мы переместим треугольник BCD влево к стороне AE то мы получим прямоугольник с шириной h и длиной a. А площадь прямоугольника равна произведению длины и ширины.
S=ah\displaystyle {S=ah}
Подставим ранее выведенную формулу стороны через радиус и угол
S=ah=2Rsin(α)×2R=4R2sin(α)\displaystyle {S=ah=\frac{2R}{sin(\alpha)} \times 2R = \frac{4R^2}{sin(\alpha)}}
S=4R2sin(α)\displaystyle {S=\frac{4R^2}{sin(\alpha)}}
Подставим значения и вычислим
S=4×152sin(1)=51568.819648694\displaystyle {S=\frac{4 \times 15^2}{sin(1)}=51568.819648694}
Площадь ромба через радиус 15 вписанной окружности и угол 1 градус между сторонами равна 51568.819648694
Площадь ромба через радиус вписанной окружности и угол между сторонами
Введите радиус окружности R
Введите угол между сторонами α
Ссылка на результат
https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-romba/cherez-radius-vpisannoj-okruzhnosti-i-ugol-mezhdu-storonami?n1=15&n2=1
Вычислить площадь ромба через радиус 1 вписанной окружности и угол между сторонами 82
Вычислить площадь ромба через радиус 9 вписанной окружности и угол между сторонами 165
Вычислить площадь ромба через радиус 44 вписанной окружности и угол между сторонами 155
Вычислить площадь ромба через радиус 49 вписанной окружности и угол между сторонами 133
Вычислить площадь ромба через радиус 34 вписанной окружности и угол между сторонами 96
Вычислить площадь ромба через радиус 5 вписанной окружности и угол между сторонами 36
Вычислить площадь ромба через радиус 45 вписанной окружности и угол между сторонами 179
Похожие калькуляторы
Площадь ромба через угол и противолежащую диагональ
Площадь ромба через угол и диагональ из этого угла
Площадь ромба через радиус вписанной окружности и сторону
Площадь ромба по стороне и углу между сторонами
Площадь ромба по стороне и высоте
Площадь ромба по диагоналям