Вычислить площадь ромба с диагоналями 33 и 4
Дано
Ромб с диагоналями 33 и 4
Задача
Вычислить площадь ромба
Решение
Диагонали ромба в точке пересечения делятся пополам и делят ромб на четыре равных треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
Подставим значения и вычислим
Площадь ромба с диагоналями 33 и 4 равна 66
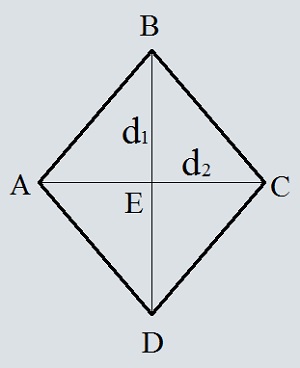
Введите диагональ d1
Введите диагональ d2
Ссылка на результат
https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-romba/po-diagonalyam?n1=33&n2=4
Вычислить площадь ромба по диагоналям 15 и 48
Вычислить площадь ромба по диагоналям 45 и 10
Вычислить площадь ромба по диагоналям 28 и 35
Вычислить площадь ромба по диагоналям 30 и 27
Вычислить площадь ромба по диагоналям 1 и 35
Вычислить площадь ромба по диагоналям 11 и 47
Вычислить площадь ромба по диагоналям 31 и 48
Вычислить площадь ромба по диагоналям 45 и 10
Вычислить площадь ромба по диагоналям 28 и 35
Вычислить площадь ромба по диагоналям 30 и 27
Вычислить площадь ромба по диагоналям 1 и 35
Вычислить площадь ромба по диагоналям 11 и 47
Вычислить площадь ромба по диагоналям 31 и 48
Похожие калькуляторы