Вычислить площадь ромба по стороне 14 и углу между сторонами 4 градуса

Дано

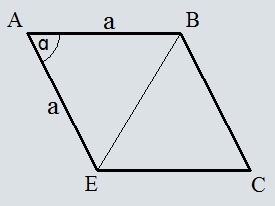
Ромб со стороной 14 и углом между сторонами 4 градуса

Задача

Вычислить площадь ромба

Решение

Т.к. треугольники ABE и BCE равны, соответственно углы EAB и BCE тоже равны.

Площадь треугольника равна половине произведения сторон на синус угла между ними.

\displaystyle {S \scriptsize ABE \normalsize =\frac{1}{2} \times a^2sin(\alpha)}

\displaystyle {S \scriptsize BCE \normalsize =\frac{1}{2} \times a^2sin(\alpha)}

\displaystyle {S \scriptsize ABCE \normalsize =S \scriptsize ABE \normalsize + S \scriptsize BCE \normalsize =\frac{1}{2} \times a^2sin(\alpha)+\frac{1}{2} \times a^2sin(\alpha)=a^2sin(\alpha)}

\displaystyle {S \scriptsize ABCE \normalsize=a^2sin(\alpha)}

Подставим значения и вычислим

\displaystyle {S \scriptsize ABCD \normalsize =14^2 \times sin(4)=13.6722688538}

Площадь ромба по стороне 14 и углу между сторонами 4 градуса равна 13.6722688538

Введите сторону ромба a

Введите угол α

Ссылка на результат

https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-romba/po-storone-i-uglu-mezhdu-storonami?n1=14&n2=4

Похожие калькуляторы