Найти длину окружности если сторона вписанного правильного семиугольника равна 6
Дано:
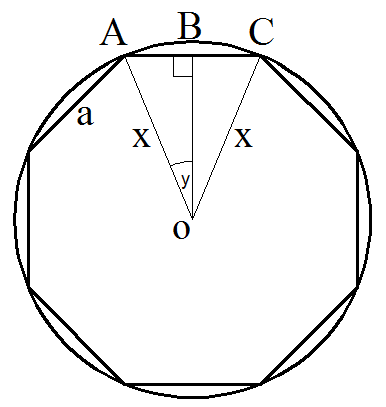
Окружность с вписанным в неё правильным семиугольником
Сторона правильного семиугольника a = 6
Решение:
Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Т.к. они одинаковые обозначим их за x. Т.к. вершины лежат на окружности то длина этих отрезков и будет радиусом окружности.
В итоге у нас получится равнобедренный треугольник ACO с двумя равными сторонами AO и CO.
Проведём высоту OB
Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.
y=180/n
AB=a/2
Из прямоугольного треугольника ABO следует
Выразим x
Т.к. x=R
Длина окружности со стороной 6 правильного семиугольника вписанного в эту окружность равна 43.4437943212
Введите сторону многоугольника a
Введите количество вершин многоугольника n
Ссылка на результат
https://calc-best.ru/matematicheskie/dlina-okruzhnosti/po-storone-vpisannogo-pravilnogo-mnogougolnika?n1=6&n2=7
Вычислить длину окружности если сторона вписанного правильного семиугольника равна 5
Вычислить длину окружности если сторона вписанного правильного треугольника равна 34
Вычислить длину окружности если сторона вписанного правильного десятиугольника равна 18
Вычислить длину окружности если сторона вписанного правильного шестиугольника равна 2
Вычислить длину окружности если сторона вписанного правильного пятиугольника равна 11
Вычислить длину окружности если сторона вписанного правильного пятиугольника равна 47
Вычислить длину окружности если сторона вписанного правильного четырёхугольника равна 43
Вычислить длину окружности если сторона вписанного правильного треугольника равна 34
Вычислить длину окружности если сторона вписанного правильного десятиугольника равна 18
Вычислить длину окружности если сторона вписанного правильного шестиугольника равна 2
Вычислить длину окружности если сторона вписанного правильного пятиугольника равна 11
Вычислить длину окружности если сторона вписанного правильного пятиугольника равна 47
Вычислить длину окружности если сторона вписанного правильного четырёхугольника равна 43
Похожие калькуляторы