Вычислить площадь прямоугольника по диагонали 13 и углу между диагоналями 147 градусов

Дано

Прямоугольник с диагональю 13 и углу между диагоналями 147 градусов

Задача

Вычислить площадь прямоугольника

Решение

Так как площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Так как sin(180-α)=sin(α) перепишем формулу выше

Сложим формулы всех 4 треугольников

Подставим значения и вычислим

Площадь прямоугольника по диагонали 13 и углу 147 градусов равна 46.0219984588

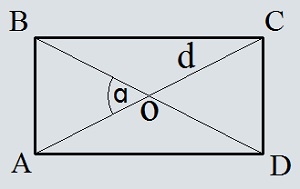
Введите диагональ d

Введите угол α

Ссылка на результат

https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-pryamougolnika/po-diagonalyam-i-uglu-mezhdu-nimi?n1=13&n2=147

Похожие калькуляторы