Найти длину окружности если сторона описанного правильного пятиугольника равна 4

Дано:

Окружность с описанным правильным пятиугольником

Сторона правильного пятиугольника a = 4

Решение:

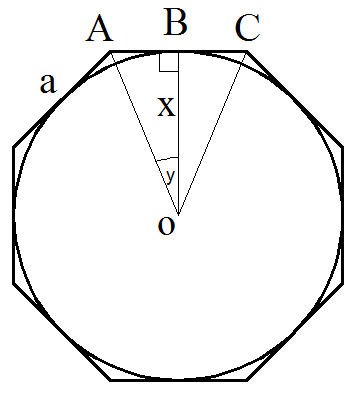
Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Получится равнобедренный треугольник ACO. С вершины O треугольника проведём высоту. Которая разделит сторону AC пополам в точке B.

Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.

y=180/n

AB=a/2

Из прямоугольного треугольника ABO следует

\displaystyle {tg(y)=\frac{AB}{BO}}

\displaystyle {tg(180/n)=\frac{a/2}{x}}

Выразим x

\displaystyle {x=\frac{a}{2tg(180/n)}}

Т.к. x=R

\displaystyle {P=2\pi R= \frac{\pi a}{tg(180/n)}}

\displaystyle {P= \frac{\pi a}{tg(180/n)}}

\displaystyle {P= \frac{{3.1415926536}\times 4}{tg(180/5)}=17.2961253195}

Длина окружности со стороной 4 правильного пятиугольника описанного около неё равна 17.2961253195

Введите сторону многоугольника a

Введите количество вершин многоугольника n

Длина окружности по стороне описанного правильного многоугольника

Ссылка на результат

https://calc-best.ru/matematicheskie/dlina-okruzhnosti/po-storone-opisannogo-pravilnogo-mnogougolnika?n1=4&n2=5

Вычислить длину окружности если сторона описанного правильного восьмиугольника равна 26
Вычислить длину окружности если сторона описанного правильного шестиугольника равна 10
Вычислить длину окружности если сторона описанного правильного треугольника равна 37
Вычислить длину окружности если сторона описанного правильного семиугольника равна 50
Вычислить длину окружности если сторона описанного правильного шестиугольника равна 48
Вычислить длину окружности если сторона описанного правильного восьмиугольника равна 19
Вычислить длину окружности если сторона описанного правильного семиугольника равна 31

Похожие калькуляторы

Длина окружности по стороне вписанного правильного многоугольника

Длина окружности по стороне описанного около окружности правильного треугольника

Длина окружности по стороне вписанного правильного треугольника

Длина окружности по стороне описанного около окружности квадрата

Длина окружности по стороне вписанного квадрата

Длина окружности по площади

Длина окружности по диаметру

Длина окружности по радиусу