Найти длину окружности если сторона описанного правильного треугольника равна 32
Дано:
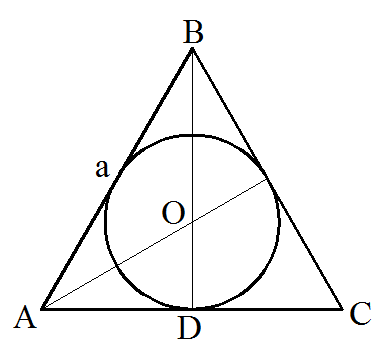
Окружность с вписанным в неё правильным треугольником
Сторона правильного треугольника a = 32
Решение:
Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.
Из этого следует что нам нужно найти радиус окружности, а он будет равен 1/3 от медианы(высоты) BD т.е. OD.
По теореме Пифагора найдём BD.
Подставим полученный радиус в формулу окружности по радиусу
Длина окружности со стороной 32 правильного треугольника описанного около этой окружности равна 58.0415796555
Введите сторону треугольника a
Ссылка на результат
https://calc-best.ru/matematicheskie/dlina-okruzhnosti/po-storone-opisannogo-pravilnogo-treugolnika?n1=32
Вычислить длину окружности если сторона описанного правильного треугольника равна 79
Вычислить длину окружности если сторона описанного правильного треугольника равна 43
Вычислить длину окружности если сторона описанного правильного треугольника равна 32
Вычислить длину окружности если сторона описанного правильного треугольника равна 58
Вычислить длину окружности если сторона описанного правильного треугольника равна 11
Вычислить длину окружности если сторона описанного правильного треугольника равна 91
Вычислить длину окружности если сторона описанного правильного треугольника равна 99
Вычислить длину окружности если сторона описанного правильного треугольника равна 43
Вычислить длину окружности если сторона описанного правильного треугольника равна 32
Вычислить длину окружности если сторона описанного правильного треугольника равна 58
Вычислить длину окружности если сторона описанного правильного треугольника равна 11
Вычислить длину окружности если сторона описанного правильного треугольника равна 91
Вычислить длину окружности если сторона описанного правильного треугольника равна 99
Похожие калькуляторы