Вычислить площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника 2 и 4

Дано

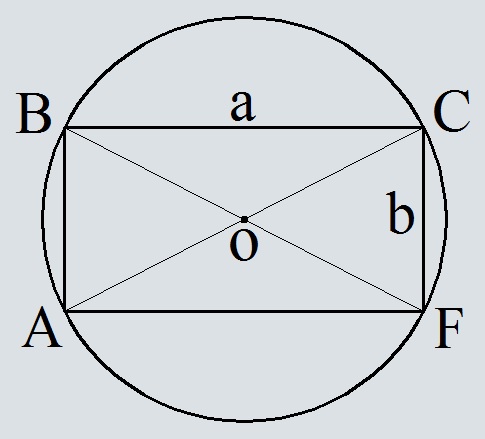
Окружность с вписанным прямоугольником

Стороны прямоугольника равны 2 и 4

Задача

Вычислить площадь круга

Решение

Диагонали прямоугольника пересекаются в центре окружности. Соответственно диагональ равна диаметру.

AC=BF=D

Из треугольника BCF по теореме пифагора вычислим BF=D по катетам BC=a и CF=b.

\displaystyle {D^2=a^2+b^2}

Подставим полученный диаметр в формулу площади окружности

\displaystyle {S=\pi R^2=\frac{\pi D^2}{4}=\frac{\pi(a^2+b^2)}{4}}

\displaystyle {S=\frac{\pi(a^2+b^2)}{4}}

Подставим значения и вычислим

\displaystyle {S=\frac{3.14 \times (2^2+4^2)}{4}=15.70}

Площадь круга описанного около прямоугольника, вычисленная по сторонам этого прямоугольника 2 и 4 равна 15.70

Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника

Введите сторону a

Введите сторону b

Ссылка на результат

https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-kruga/opisannogo-okolo-pryamougolnika-vychislennaya-po-storonam-pryamougolnika?n1=2&n2=4

Похожие калькуляторы

Площадь круга описанного около прямоугольного треугольника, по катетам треугольника

Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника

Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника

Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника

Площадь круга вписанного в равносторонний треугольник, по площади треугольника

Площадь круга вписанного в равносторонний треугольник, по высоте треугольника

Площадь круга вписанного в равносторонний треугольник, по стороне треугольника

Площадь круга описанного около равностороннего треугольника, по площади треугольника

Площадь круга описанного около равностороннего треугольника, по высоте треугольника

Площадь круга описанного около равностороннего треугольника, по стороне треугольника

Площадь круга по площади квадрата вписанного в этот круг

Площадь круга по стороне квадрата вписанного в этот круг

Площадь круга по длине окружности

Площадь круга по диаметру

Площадь круга по радиусу