Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 13 и 10

Дано
Прямоугольный треугольник с вписанной окружностью
Катеты треугольника равны 13 и 10
Задача
Вычислить площадь круга
Решение
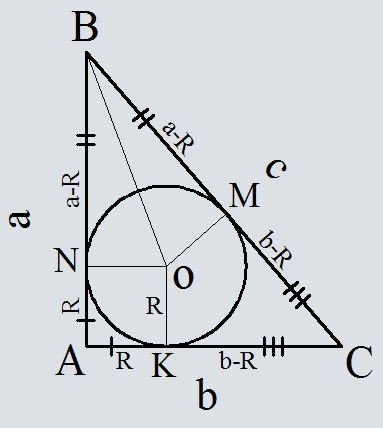
Т.к. отрезки касательных к окружности проведённые из одной точки равны
AN=AK=R
NB=BM=a-R
KC=CM=b-R
BC=c=BM+CM=a-R+b-R
c=a-R+b-R
Выведем радиус R
2R=a+b-c
R=a+b−c2\displaystyle {R=\frac{a+b-c}{2}}
По теореме пифагора выведем гипотенузу c
c2=a2+b2\displaystyle {c^2=a^2+b^2}
c=a2+b2\displaystyle {c=\sqrt{a^2+b^2}}
Подставим в выведенную ранее формулу радиуса гипотенузу
R=a+b−c2=a+b−a2+b22\displaystyle {R=\frac{a+b-c}{2}=\frac{a+b-\sqrt{a^2+b^2}}{2}}
Подставим полученный радиус в формулу площади окружности
S=πR2=π(a+b−a2+b22)2\displaystyle {S=\pi R^2=\pi \Big(\frac{a+b-\sqrt{a^2+b^2}}{2}\Big)^2}
S=π(a+b−a2+b22)2\displaystyle {S=\pi \Big(\frac{a+b-\sqrt{a^2+b^2}}{2}\Big)^2}
Подставим значения и вычислим
S=3.14×(13+10−132+1022)2=34.1819650518\displaystyle {S=3.14 \times \Big(\frac{13+10-\sqrt{13^2+10^2}}{2}\Big)^2=34.1819650518}
Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 13 и 10 равна 34.1819650518
Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
Введите катет a
Введите катет b
Ссылка на результат
https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-kruga/vpisannogo-v-pryamougolnyj-treugolnik-po-katetam-treugolnika?n1=13&n2=10
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 31 и 47
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 36 и 1
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 4 и 18
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 26 и 25
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 26 и 15
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 4 и 9
Вычислить площадь круга вписанного в прямоугольный треугольник, по катетам треугольника 37 и 33
Похожие калькуляторы
Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Площадь круга вписанного в равносторонний треугольник, по площади треугольника
Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
Площадь круга описанного около равностороннего треугольника, по площади треугольника
Площадь круга описанного около равностороннего треугольника, по высоте треугольника
Площадь круга описанного около равностороннего треугольника, по стороне треугольника
Площадь круга по площади квадрата вписанного в этот круг
Площадь круга по стороне квадрата вписанного в этот круг
Площадь круга по длине окружности
Площадь круга по диаметру
Площадь круга по радиусу