Вычислить площадь круга вписанного в равносторонний треугольник, по стороне этого треугольника равной 66

Дано
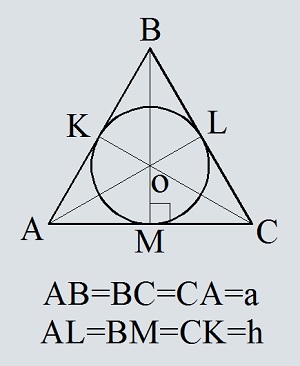
Равносторонний треугольник с вписанной окружностью
Сторона треугольника a = 66
Задача
Вычислить площадь круга
Решение
В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой. Все они пересекаются в одной точке и делятся ею в отношении 1:2. Эта точка является центром окружности вписанной в этот треугольник.
R=OM=13BM\displaystyle {R=OM=\frac{1}{3}BM}
Т.к. BM=h перепишем формулу выше
R=OM=13h\displaystyle {R=OM=\frac{1}{3}h}
h мы вычислим по теореме пифагора из треугольника ABM. AB=a; AM=a/2
h2=a2−(a2)2=3a24\displaystyle {h^2=a^2-\Big(\frac{a}{2}\Big)^2=\frac{3a^2}{4}}
Подставим в формулу площади круга радиус через h
S=πR2=19πh2\displaystyle {S=\pi R^2=\frac{1}{9} \pi h^2}
Подставим выведенную ранее высоту h
S=19π×3a24=πa212\displaystyle {S=\frac{1}{9} \pi \times \frac{3a^2}{4} = \frac{\pi a^2}{12}}
S=πa212\displaystyle {S=\frac{\pi a^2}{12}}
Подставим значение и вычислим
S=3.14×66212=1139.82\displaystyle {S=\frac{3.14 \times 66^2}{12}=1139.82}
Площадь круга вписанного в равносторонний треугольник, со стороной этого треугольника 66 равна 1139.82
Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
Введите сторону равностороннего треугольника a
Ссылка на результат
https://calc-best.ru/matematicheskie/ploshchadi-figur/ploshchad-kruga/vpisannogo-v-ravnostoronnij-treugolnik-po-storone-treugolnika?n=66
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 45
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 33
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 32
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 54
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 46
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 97
Вычислить площадь круга вписанного в равносторонний треугольник, если сторона этого треугольника равна 33
Похожие калькуляторы
Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Площадь круга вписанного в равносторонний треугольник, по площади треугольника
Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
Площадь круга описанного около равностороннего треугольника, по площади треугольника
Площадь круга описанного около равностороннего треугольника, по высоте треугольника
Площадь круга описанного около равностороннего треугольника, по стороне треугольника
Площадь круга по площади квадрата вписанного в этот круг
Площадь круга по стороне квадрата вписанного в этот круг
Площадь круга по длине окружности
Площадь круга по диаметру
Площадь круга по радиусу